Question

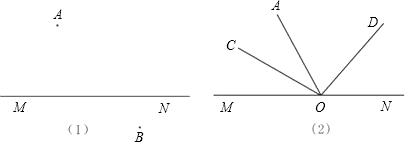
如图（1），已知A、B位于直线MN的两侧，请在直线MN上找一点P，使PA+PB最小，并说明依据．
如图（2），动点O在直线MN上运动，连接AO，分别画∠AOM、∠AON的角平分线OC、OD，请问∠COD的度数是否发生变化？若不变，求出∠COD的度数；若变化，说明理由．

Answer 1

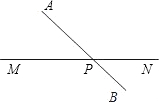解：（1）如图，连接AB交MN于点P，则P就是所求的点．理由：两点之间线段最短，

（2）∠COD的度数不会变化，
∵OC是∠AOM的平分线，
，∴∠COA=∠AOM，
∵OD是∠AON的平分线，
∴∠AOD=∠AON，
∵∠AOM+∠AON=180°，
∴∠COA+∠AOD=∠AOM+∠AON=（∠AOM+∠AON）=90°．
分析：（1）显然根据两点之间，线段最短．连接两点与直线的交点即为所求作的点．
（2）根据角平分线的概念以及邻补角的概念即可证明．
点评：求两点之间的最短距离时，注意两点之间，线段最短；互为邻补角的两个角的角平分线互相垂直．