Question

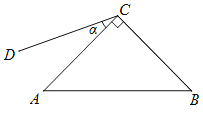
【题目】如图1,在△ADC中,,,将△ADC沿直线AC对折得△ABC,点E为AB边上一动点(与点A,B不重合),连接CE,将射线CE绕点C顺时针旋转120°,交射线AD于点F.

(1)求的长度；

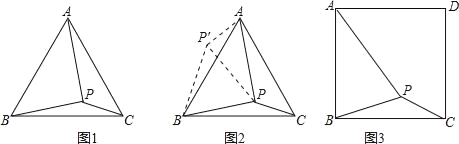
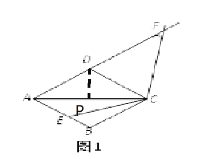
(2)如图2,当E为AB中点时,求CF的长度；

(3)用等式表示线段AE,AF与AC之间的数量关系,并加以证明.

Answer 1

【答案】（1）；（2）CF的长为；（3），详见解析.

【解析】

（1）过点D作DP⊥AC,垂足为P ，利用等腰三角形的性质和直角三角形的性质求出,，再利用勾股定理进行计算即可.

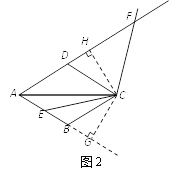
(2)作CH⊥AF于点H, CG⊥AB于点G ，根据题意得到△ADC≌△ABC，再利用利用等腰三角形的性质和直角三角形的性质得到△CFH≌△CEG ，再根据勾股定理即可解答；

（3）先由（2）证明Rt△ACH≌Rt△ACG ，再利用三角函数即可解答.

解:(1)如图1, 过点D作DP⊥AC,垂足为P

∵,

∴,

∴

∴；

(2)如图2,作CH⊥AF于点H, CG⊥AB于点G

∴

由题意,得△ADC≌△ABC

∴,

∵

∴,

∵

∴

∴△CFH≌△CEG

∴

在Rt△CBG中,,

∴,

在Rt△CEG中,

∴

∴CF的长为；

(3)线段AE,AF与AC之间的数量关系为:

证明如下:

由(2)得△CFH≌△CEG

∴

∵,

∴Rt△ACH≌Rt△ACG

∴

在Rt△ACG中,

∴

∴.