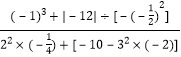��Ŀ����
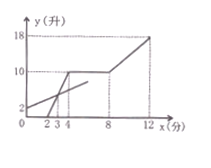
����Ŀ����ͼ����ʾ����ֱ������ABCD�У���BAD=90�㣬E��ֱ��AB��һ�㣬��E��ֱ��l��BC����ֱ��CD�ڵ�F����ֱ��l����ƽ�ƣ���ƽ�ƾ���BEΪt��t��0����ֱ������ABCD��ֱ��lɨ���������ͼ����Ӱ���֣�ΪS��S����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ�N�������Ϊ4��
��Ϣ��ȡ
��1�������ϵij�AB=��
��2��ֱ������ABCD�����=��
ͼ������
��3��д��ͼ��������NQ��ʾ��ʵ�����壻
��4����2��t��4ʱ����S����t�ĺ�����ϵʽ��
������
��5����tΪ��ֵʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
���𰸡�
��1��2
��2��12
��3��
�⣺��ƽ�ƾ���BE���ڵ���4ʱ��ֱ������ABCD��ֱ��lɨ���������Ϊ12
��4��
�⣺��2��t��4ʱ����ͼ��ʾ��
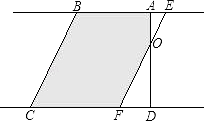
ֱ������ABCD��ֱ��lɨ�������S=Sֱ������ABCD��SRt��DOF
=12�� ![]() ��4��t����2��4��t��=��t2+8t��4
��4��t����2��4��t��=��t2+8t��4
��5��
�⣺�ٵ�0��t��2ʱ����4t����12��4t��=1��3�����t= ![]() ��
��
�ڵ�2��t��4ʱ���У���t2+8t��4����[12������t2+8t��4��]=3��1��
��t2��8t+13=0��
���t=4�� ![]() ��t=4+
��t=4+ ![]() ����ȥ����
����ȥ����
��t= ![]() ��t=4��
��t=4�� ![]() ʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3
ʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3
���������⣺������ã���1��AB=2����2��S����ABCD=12��
��1������ͼ�ڿ�֪����0��t��2ʱ��E���߶�AB���˶���������A��B�غϣ����ڴ��ڼ�E���˶���2����˿����AB�ij�Ϊ2����2������ͼ�ο�֪����2��t��4ʱ��E��AB���ӳ����ϣ���F��D����࣬���ڼ�E���˶���2������µ׳�Ϊ2+2=4������t=2ʱ���غϲ��ֵ����Ϊ8��������εĸ�Ϊ4��������ε����Ϊ ![]() ����2+4����4=12����3����t��4ʱ��ֱ��l������û�н��㣬���ɨ���������Ϊ���ε����12����4����2��t��4ʱ��ֱ��ɨ�����εIJ����Ǹ�����Σ������ֱ��l��AD�Ľ���Ϊ0����ô�غϲ��ֵ�����������ε������ȥ������OFD���������ã����ε�����ڣ�2�����Ѿ���ã�������OFD�У��ױ�DF=4��t����DF�ϵĸߣ�����DF�ij��͡�BCD������ֵ������ɴ˿ɵó�S��t�ĺ�����ϵʽ����5������Ҫ��������ۣ��ٵ�0��t��2ʱ���غϲ��ֵ�ƽ���ı��ε������ֱ������AEFD�����=1��3���ݴ˿����t��ֵ���ڵ�2��t��4ʱ���غϲ��ֵ�����ε������������OFD�����=3��1���ɴ˿����t��ֵ��
����2+4����4=12����3����t��4ʱ��ֱ��l������û�н��㣬���ɨ���������Ϊ���ε����12����4����2��t��4ʱ��ֱ��ɨ�����εIJ����Ǹ�����Σ������ֱ��l��AD�Ľ���Ϊ0����ô�غϲ��ֵ�����������ε������ȥ������OFD���������ã����ε�����ڣ�2�����Ѿ���ã�������OFD�У��ױ�DF=4��t����DF�ϵĸߣ�����DF�ij��͡�BCD������ֵ������ɴ˿ɵó�S��t�ĺ�����ϵʽ����5������Ҫ��������ۣ��ٵ�0��t��2ʱ���غϲ��ֵ�ƽ���ı��ε������ֱ������AEFD�����=1��3���ݴ˿����t��ֵ���ڵ�2��t��4ʱ���غϲ��ֵ�����ε������������OFD�����=3��1���ɴ˿����t��ֵ��