Question

【题目】在平面直角坐标系xOy中，抛物线与轴交于点A，顶点为点B，点C与点A关于抛物线的对称轴对称．

（1）求直线BC的解析式；

（2）点D在抛物线上，且点D的横坐标为4．将抛物线在点A，D之间的部分（包含点A，D）记为图象G，若图象G向下平移（）个单位后与直线BC只有一个公共点，求的取值范围．

Answer 1

【答案】（1）（2）．

【解析】

试题（1）首先根据抛物线求出与轴交于点A，顶点为点B的坐标，然后求出点A关于抛物线的对称轴对称点C的坐标，设设直线BC的解析式为．代入点B，点C的坐标，然后解方程组即可；（ 2）求出点D、E、F的坐标，设点A平移后的对应点为点，点D平移后的对应点为点．当图象G向下平移至点与点E重合时， 点在直线BC上方，此时t=1；当图象G向下平移至点与点F重合时，点在直线BC下方，此时t=3．从而得出.

试题解析：解：（1）∵抛物线与轴交于点A，

∴点A的坐标为（0，2）． 1分

∵，

∴抛物线的对称轴为直线，顶点B的坐标为（1，）． 2分

又∵点C与点A关于抛物线的对称轴对称，

∴点C的坐标为(2，2)，且点C在抛物线上．

设直线BC的解析式为．

∵直线BC经过点B（1，）和点C(2，2)，

∴ 解得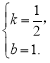

∴直线BC的解析式为

． 3分

（2）∵抛物线中，

当时，，

∴点D的坐标为(4，6)． 4分

∵直线中，

当时，，

当时，，

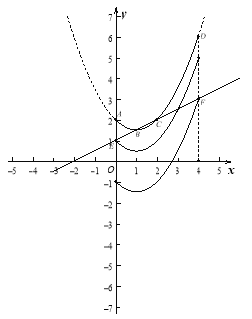
∴如图，点E的坐标为(0，1)，

点F的坐标为(4，3)．

设点A平移后的对应点为点，点D平移后的对应点为点．

当图象G向下平移至点与点E重合时， 点在直线BC上方，

此时t=1； 5分

当图象G向下平移至点与点F重合时，点在直线BC下方，此时t=3．

6分

结合图象可知，符合题意的t的取值范围是． 7分