Question

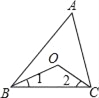
【题目】（1）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，若∠A=42°，求∠BOC的度数；

（2）把（1）中∠A=42°这个条件去掉，试探索∠BOC和∠A之间有怎样的数量关系．

Answer 1

【答案】（1）111°（2）证明见解析

【解析】试题分析：（1）根据角平分线的定义得到∠1=∠ABC，∠2=∠ACB，再根据三角形内角和定理得到∠1+∠2+∠COB=180°，∠ABC+∠ACB+∠A=180°，经过变形后得到∠BOC=90°+∠A，然后把∠A=40°代入计算即可；

（2）利用上面的证明方法，直接可证明∠BOC=90°+∠A．

试题解析：（1）∵∠A=42°，

∴∠ABC+∠ACB=180°﹣∠A=138°，

∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线，

∴∠1=∠ABC，∠2=∠ACB，

∴∠1+∠2=（∠ABC+∠ACB）=×138°=69°，

∴∠BOC=180°﹣（∠1+∠2）=180°﹣69°=111°；

（2）∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线，

∴∠1=∠ABC，∠2=∠ACB，

∴∠1+∠2=（∠ABC+∠ACB）=（180°﹣∠A），

∴∠BOC=180°﹣（∠1+∠2）=180°﹣（180°﹣∠A）=90°+∠A．