题目内容
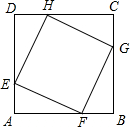如图，正方形EFGH的四个顶点在正方形ABCD的边上，若AB=a，EF=b，则△AEF的内切圆半径为分析：根据正方形的性质可以证明△AEF≌△BFG，得AE=BF，再根据直角三角形内切圆的半径等于两条直角边的和减去斜边的差的一半进行计算．
解答：解：∵四边形ABCD和四边形EFGH都是正方形，
∴∠A=∠B=∠EFG=90°，EF=FG，
∴∠AFE=∠BGF，
∴△AEF≌△BFG，
∴AE=BF，
∴AE+AF=AB=a，
∴△AEF的内切圆半径为
．
故答案为
．
∴∠A=∠B=∠EFG=90°，EF=FG，
∴∠AFE=∠BGF，
∴△AEF≌△BFG，
∴AE=BF，
∴AE+AF=AB=a，
∴△AEF的内切圆半径为
| a-b |
| 2 |
故答案为
| a-b |
| 2 |
点评：此题考查了正方形的性质、全等三角形的判定和性质以及直角三角形内切圆的半径公式：直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
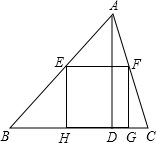如图，正方形EFGH内接于△ABC，设BC=
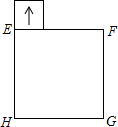如图，正方形EFGH的边长是3cm，一个边长为1cm的小正方形沿着正方形EFGH的边EF→FG→GH→HE连续地翻转，那么这个小正方形回到起始位置时，它的方向是下图的（ ）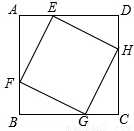
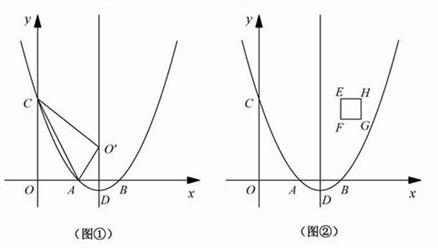
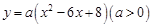的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．
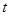个单位长度时，正方形EFGH上是否存在一点P（包括正方形的边界），使得四条线段PA、PB、PC、PD能够构成平行四边形？如果存在，请求出