题目内容
如果在一个正方体的每个面内写一个正整数,然后,在每个顶点处再写一个数,该数等于过这个顶点的三个面内的数的乘积,那么当该正方体各个顶点处的数之和是290时,各个面内的数之和等于( )
分析:先设面内的数为a1,a2…a6,点上的数为b1,b2…b8,根据题意列出a、b之间的关系式,得到(a1+a6)×(a2+a4)×(a3+a5)=290,把式中括号内的看作整体并设为x,y,z,根据这三数是整数可对290进行分解质因数,的出各种可能的数值,再求出其和即可.
解答:解:设面内的数为a1,a2…a6,点上的数为b1,b2…b8,
则b1=a1a2a3;
b2=a1a3a6;
b3=a1a4a3;
…
正方体各个顶点处的数之和是290时,(a1+a6)×(a2+a4)×(a3+a5)=290.
∵求的是他们的和,
∴把式中括号内的看作整体,
设为x,y,z,题目变为已知三数积求和,
又∵这三数是整数,
∴可以将290分解质因数,得到6种可能,即2×5×29,10×29×1,145×2×1,290×1×1,58×5×1,
∴和为36,40,148,292,64这几种可能.
故选C.
则b1=a1a2a3;
b2=a1a3a6;
b3=a1a4a3;
…
正方体各个顶点处的数之和是290时,(a1+a6)×(a2+a4)×(a3+a5)=290.
∵求的是他们的和,
∴把式中括号内的看作整体,
设为x,y,z,题目变为已知三数积求和,
又∵这三数是整数,
∴可以将290分解质因数,得到6种可能,即2×5×29,10×29×1,145×2×1,290×1×1,58×5×1,
∴和为36,40,148,292,64这几种可能.
故选C.
点评:本题考查的是分解质因数,能把290分解质因数得到所有可能的式子是解答此题的关键.

练习册系列答案
相关题目

 、2
、2 ;
;
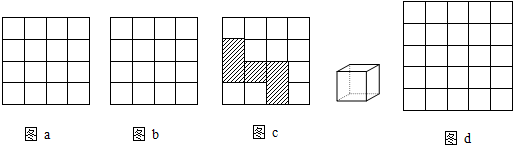
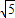 、2
、2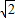 ;
;