题目内容
2.若方程x2-2x+m=0没有实数根,则实数m为( )| A. | m≤1 | B. | m<1 | C. | m>1 | D. | m≥1 |
分析 根据方程没有实数根,得到根的判别式小于0列出关于m的不等式,求出不等式的解集即可得到m的范围.
解答 解:根据方程没有实数根,得到△=b2-4ac=4-4m<0,
解得:m>1.
故选C.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.上面的结论反过来也成立.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
12.在Rt△ABC中,∠C=90°,BC=6,sinA=$\frac{3}{5}$,则AB的值是( )
| A. | 4 | B. | 5 | C. | 8 | D. | 10 |
13.多项式x2-4分解因式的结果是( )
| A. | (x+2)(x-2) | B. | (x-2)2 | C. | (x+4)(x-4) | D. | x(x-4) |
10.如果下列二次根式中有一个与$\sqrt{a}$是同类二次根式,那么这个根式是( )
| A. | $\sqrt{2}$a | B. | $\sqrt{3{a}^{2}}$ | C. | $\sqrt{{a}^{3}}$ | D. | $\sqrt{{a}^{4}}$ |
17.将57000000用科学记数法表示应为( )
| A. | 570×105 | B. | 57×106 | C. | 5.7×107 | D. | 0.57×108 |
14.下列各式计算结果正确的是( )
| A. | a+a=a2 | B. | (a-1)2=a2-1 | C. | a•a=a2 | D. | (3a)3=9a2 |
11.如果点A(x1,y1),B(x2,y2)都在一次函数y=-x+3的图象上,并且x1<x2,那么y1与y2的大小关系正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法判断 |
12.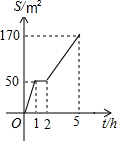 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )
 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )| A. | 100m2 | B. | 80m2 | C. | 50m2 | D. | 40m2 |