题目内容
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 在
在![]() 上,且
上,且![]() ,请判断并写出
,请判断并写出![]() 与
与![]() 之间的关系,并进行证明.
之间的关系,并进行证明.

【答案】AE=CF,AE⊥CF
【解析】
根据“SAS”可判断△ABE≌△CBF,根据全等的性质有AE=CF,∠1=∠2(详解中图形),根据对顶角相等有∠3=∠4,再利用三角形内角和定理可得到∠CHE=∠ABE=90°,则AE⊥CF.
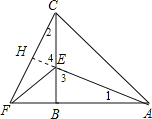
解:![]() 与
与![]() 之间的关系:AE=CF,AE⊥CE.理由如下:
之间的关系:AE=CF,AE⊥CE.理由如下:
延长AE交CF于H,如上图,
∵∠ABC=90°,
∴![]() ,
,
在△ABE和△CBF中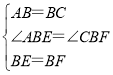
∴△ABE≌△CBF(SAS),
∴AE=CF,∠1=∠2,
∵∠3=∠4(对顶角相等),∠CHE=180°-∠2-∠4,∠ABE=180°-∠1-∠3
∴∠CHE=∠ABE=90°,
∴EH⊥CF,即AE⊥CF
则有AE与CF垂直且相等.

 阅读快车系列答案
阅读快车系列答案【题目】已知关于x的代数式x2+bx+c,设代数式的值为y.下表中列出了当x分别取﹣1,0,1,2,3,4,5,…m,m+1…时对应的y值.
x | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | m | m+1 | |||
y | 10 | 5 | 2 | 1 | 2 | 5 | n | p | q |
(1)表中n的值为 ;
(2)当x= 时,y有最小值,最小值是 ;
(3)比较p与q的大小.
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
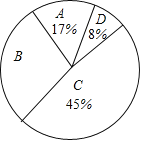
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。




