题目内容
【题目】如图1，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．
（1）当t= 时，△PQR的边QR经过点B；
（2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式；
（3）如图2，过定点E（5，0）作EF⊥BC，垂足为F，当△PQR的顶点R落在矩形OABC的内部时，过点R作x轴、y轴的平行线，分别交EF、BC于点M、N，若∠MAN=45°，求t的值．
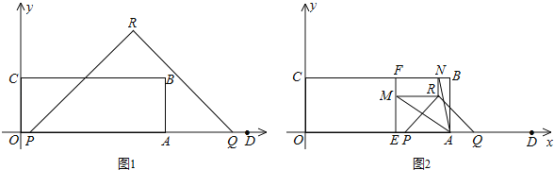
【答案】(1)1秒
(2)
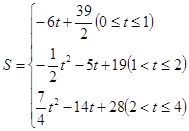
(3)t的值为（8﹣2
）
【解析】试题分析：（1）△PQR的边QR经过点B时，△ABQ构成等腰直角三角形，则有AB=AQ，由此列方程求出t的值；
（2）在图形运动的过程中，有三种情形，需要分类讨论，避免漏解；
（3）由已知可得ABFE为正方形；其次通过旋转，由三角形全等证明MN=EM+BN；设EM=m，BN=n，在Rt△FMN中，由勾股定理得到等式：mn+3（m+n）﹣9=0，由此等式列方程求出时间t的值．
试题解析：（1）△PQR的边QR经过点B时，△ABQ构成等腰直角三角形，
∴AB=AQ，即3=4﹣t，
∴t=1．
即当t=1秒时，△PQR的边QR经过点B．
（2）①当0≤t≤1时，如答图1﹣1所示．
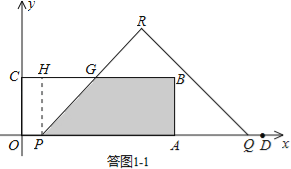
设PR交BC于点G，
过点P作PH⊥BC于点H，则CH=OP=2t，GH=PH=3．
S=S矩形OABC﹣S梯形OPGC
=8×3﹣
（2t+2t+3）×3
=﹣6t+
；
②当1＜t≤2时，如答图1﹣2所示．
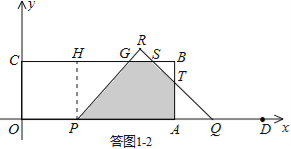
设PR交BC于点G，RQ交BC、AB于点S、T．
过点P作PH⊥BC于点H，则CH=OP=2t，GH=PH=3．
QD=t，则AQ=AT=4﹣t，
∴BT=BS=AB﹣AQ=3﹣（4﹣t）=t﹣1．
S=S矩形OABC﹣S梯形OPGC﹣S△BST
=8×3﹣（2t+2t+3）×3﹣（t﹣1）2
=﹣t2﹣5t+19；
③当2＜t≤4时，如答图1﹣3所示．
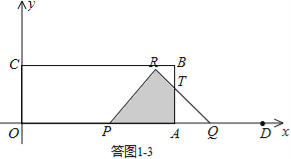
设RQ与AB交于点T，则AT=AQ=4﹣t．
PQ=12﹣3t，∴PR=RQ=
（12﹣3t）．
S=S△PQR﹣S△AQT
=PR2﹣AQ2
=
（12﹣3t）2﹣（4﹣t）2
=
t2﹣14t+28．
综上所述，S关于t的函数关系式为：
．
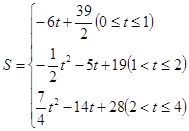（3）∵E（5，0），∴AE=AB=3，
∴四边形ABFE是正方形．
如答图2，将△AME绕点A顺时针旋转90°，得到△ABM′，其中AE与AB重合．
∵∠MAN=45°，∴∠EAM+∠NAB=45°，
∴∠BAM′+∠NAB=45°，
∴∠MAN=∠M′AN．
连接MN．在△MAN与△M′AN中，
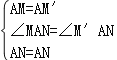
∴△MAN≌△M′AN（SAS）．
∴MN=M′N=M′B+BN
∴MN=EM+BN．
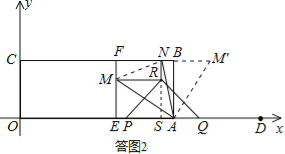
设EM=m，BN=n，则FM=3﹣m，FN=3﹣n．
在Rt△FMN中，由勾股定理得：FM2+FN2=MN2，即（3﹣m）2+（3﹣n）2=（m+n）2，
整理得：mn+3（m+n）﹣9=0． ①
延长MR交x轴于点S，则m=EM=RS=PQ=（12﹣3t），
∵QS=PQ=（12﹣3t），AQ=4﹣t，
∴n=BN=AS=QS﹣AQ=（12﹣3t）﹣（4﹣t）=﹣t+2．
∴m=3n，
代入①式，化简得：n2+4n﹣3=0，
解得n=﹣2+或n=﹣2﹣（舍去）
∴2﹣t=﹣2+
解得：t=8﹣2．
∴若∠MAN=45°，则t的值为（8﹣2）秒．
