Question

【题目】在等腰和等腰中，，，连接交于点.

(1）如图1，若：

①与的数量关系为 ；

②的度数为 ；

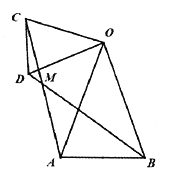
图1

（2）如图2，若：

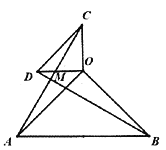
图2

①判断与之间存在怎样的数量关系？并说明理由；

②求的度数；

Answer 1

【答案】（1）①，②；（2）①，理由见解析，②.

【解析】

（1）①先证明：∠BOD=∠AOC，再证明△BOD≌△AOC（SAS），即可得AC=BD；②由△BOD≌△AOC及三角形内角和定理即可求得∠AMB=40°；
（2）①证明△BOD≌△AOC（SAS）即可得BD=AC，②根据全等三角形性质和三角形内角和定理即可求得∠AMB；

（1）如图1所示，

①∵∠AOB=∠COD
∴∠AOB+∠AOD=∠COD+∠AOD
∴∠BOD=∠AOC
在△BOD和△AOC中

∴△BOD≌△AOC（SAS）
∴AC=BD
故答案为：AC=BD，
②∵△BOD≌△AOC
∴∠OBD=∠OAC
∵∠AOB=40°，
∴∠OAB+∠OBA=180°-∠AOB=180°-40°=140°
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=140°，
∴∠MAB+ABM=140°
∵在△ABM中，∠AMB+∠MAB+∠ABM=180°，
∴∠AMB=40°
故答案为：40°；
（2）如图2所示，

①AC=BD，
∵∠AOB=∠COD=90°，
∴∠AOB+∠AOD=∠COD+∠AOD，
∴∠BOD=∠AOC，
在△BOD和△AOC中
，
∴△BOD≌△AOC（SAS）
∴BD=AC
②∵△BOD≌△AOC，
∴∠OBD=∠OAC，
又∵∠OAB+∠OBA=90°，
∠ABO=∠ABM+∠OBD，
∠MAB=∠MAO+∠OAB，
∴∠MAB+∠MBA=90°，
又∵在△AMB中，∠AMB+∠ABM+∠BAM=180°，

∴∠AMB=180°-（∠ABM+∠BAM）=180°-90°=90°；