Question

【题目】如图所示，AC⊥AB，AB=2 ，AC=2，点D是以AB为直径的半圆O上一动点，DE⊥CD交直线AB于点E，设∠DAB=α（0°＜α＜90°）．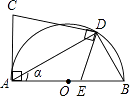
（1）当α=18°时，求 的长；
（2）当α=30°时，求线段BE的长；
（3）若要使点E在线段BA的延长线上，则α的取值范围是（直接写出答案）

Answer 1

【答案】
（1）解：连接OD，

∵α=18°，

∴∠DOB=2α=36°，

∵AB=2 ，

∴⊙O的半径为： ，

∴ 的长为： = π

（2）解：∵AB是⊙O的直径，

∴∠ADB=90°，

∵α=30°，

∴∠B=60°，

∵AC⊥AB，DE⊥CD，

∴∠CAB=∠CDE=90°，

∴∠CAD=90°﹣α=60°，

∴∠CAD=∠B，

∵∠CDA+∠ADE=∠ADE+∠BDE=90°，

∴∠CDA=∠BDE，

∴△ACD∽△BED，

∴ ，

∵AB=2 ，α=30°，

∴BD= AB= ，

∴AD= =3，

∴ ，

∴BE= ；

经检验，BE= 是原分式方程的解

（3）60°＜α＜90°
【解析】解：（3）如图，当E与A重合时， ∵AB是直径，AD⊥CD，
∴∠ADB=∠ADC=90°，
∴C，D，B共线，
∵AC⊥AB，
∴在Rt△ABC中，AB=2 ，AC=2，
∴tan∠ABC= = ，
∴∠ABC=30°，
∴α=∠DAB=90°﹣∠ABC=60°，
当E′在BA的延长线上时，如图，可得∠D′AB＞∠DAB＞60°，
∵0°＜α＜90°，
∴α的取值范围是：60°＜α＜90°．
所以答案是：60°＜α＜90°．


【考点精析】认真审题，首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)，还要掌握弧长计算公式(若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的)的相关知识才是答题的关键．