题目内容
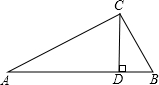在Rt△ABC中，∠C为直角，CD⊥AB于点D．BC=3，AB=5，写出其中的一对相似三角形是________和________；并写出它的面积比________．
△BCD △CAD 9：16
分析：因为直角三角形斜边上的高，把直角三角形分成的两个三角形与原三角形相似，根据相似三角形的面积比等于相似比的平方即可求解．
解答：∵∠C=90°，CD⊥AB
∴△CDB∽△ADC
∴BC：AC=3：4
∴面积比为9：16．
（答案不唯一，也可以填：①△CDB∽△ACB，面积比为9：25；②△ACD∽△ABC，面积比为16：25．）
点评：此题主要考查的是相似三角形的性质：相似三角形的面积比等于相似比的平方；找准相似三角形的对应边是解题的关键．
分析：因为直角三角形斜边上的高，把直角三角形分成的两个三角形与原三角形相似，根据相似三角形的面积比等于相似比的平方即可求解．
解答：∵∠C=90°，CD⊥AB
∴△CDB∽△ADC
∴BC：AC=3：4
∴面积比为9：16．
（答案不唯一，也可以填：①△CDB∽△ACB，面积比为9：25；②△ACD∽△ABC，面积比为16：25．）
点评：此题主要考查的是相似三角形的性质：相似三角形的面积比等于相似比的平方；找准相似三角形的对应边是解题的关键．
练习册系列答案
相关题目
已知：如图，在Rt△ABC中，∠C=90°，AC=12，BC=9，D是AB上一点，以BD为直径的⊙O切AC于E，求⊙O的半径．
如图，已知：在Rt△ABC中，∠C=90°，AB=12，点D是AB的中点，点O是△ABC的重心，则OD的长为（ ）在Rt△ABC中，已知a及∠A，则斜边应为（ ）
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，且AD：BD=9：4，则AC：BC的值为（ ）| A、9：4 | B、9：2 | C、3：4 | D、3：2 |