题目内容
 如图是某校举行数学活动节的会徽轮廓图案在直角坐标系中的大致位置,它由相同对称轴的两条抛物线组成,有下列判断:①h>0;②m>0;③a>b;④m>n,其中正确的个数有( )
如图是某校举行数学活动节的会徽轮廓图案在直角坐标系中的大致位置,它由相同对称轴的两条抛物线组成,有下列判断:①h>0;②m>0;③a>b;④m>n,其中正确的个数有( )| A、1 | B、2 | C、3 | D、4 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:根据抛物线的顶点式可得抛物线y1的顶点坐标为(h,m),则可对①②进行判断;根据二次项系数的作用可对③进行判断;比较亮个抛物线的顶点的纵坐标可对④进行判断.
解答:解:∵抛物线y1的顶点坐标为(h,m),
∴h>0,m>0,所以①②正确;
∵两个抛物线的开口都向上,
∴a>0,b>0,
而抛物线y1的开口比抛物线y2的开口大,
∴a<b,所以③错误;
∵抛物线y2的顶点坐标为(k,n),
∴m>n,所以④正确.
故选C.
∴h>0,m>0,所以①②正确;
∵两个抛物线的开口都向上,
∴a>0,b>0,
而抛物线y1的开口比抛物线y2的开口大,
∴a<b,所以③错误;
∵抛物线y2的顶点坐标为(k,n),
∴m>n,所以④正确.
故选C.
点评:本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
在
、
、π、
、0.505005000中无理数的个数为( )
| ||
| 2 |
| 1 |
| 3 |
| 9 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,图中的棱柱一共有( )
如图,图中的棱柱一共有( )| A、6个面,12条棱 |
| B、6个面,15条棱 |
| C、7个面,12条棱 |
| D、7个面,15条棱 |
一种上衣每件成本为60元,按高出成本价的25%标价出售,后因库存积压,又按标价的80%出售,每件上衣还能盈利( )
| A、0元 | B、1.5元 |
| C、4.8元 | D、5元 |
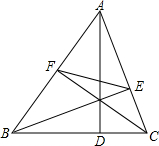 如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )
如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
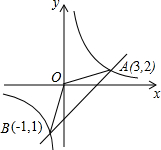 如图,反比例函数y=
如图,反比例函数y= 如图,在△ABC中,CD⊥AB于D,AC=10cm,AD=6cm,BC=
如图,在△ABC中,CD⊥AB于D,AC=10cm,AD=6cm,BC=