题目内容
17、已知：如图，在梯形ABCD中，AB∥CD，E、F为AB上两点，且AE=BF，DE=CF，EF≠CD．求证：AD=BC．
分析：首先根据等腰梯形CDEF得到∠DEF=∠CFE，再根据等角的补角相等得到∠AED=∠BFC．然后根据SAS证明△AED≌△BFC，从而证明结论．
解答：证明：∵DC∥EF，EF≠CD，
∴四边形CDEF是梯形，
∵DE=CF，
∴梯形CDEF是等腰梯形，
∴∠DEF=∠CFE，
∴∠DEA=∠CFB，
又∵AE=BF，DE=CF，
∴△AED≌△BFC，
∴AD=BC．
∴四边形CDEF是梯形，
∵DE=CF，
∴梯形CDEF是等腰梯形，
∴∠DEF=∠CFE，
∴∠DEA=∠CFB，
又∵AE=BF，DE=CF，
∴△AED≌△BFC，
∴AD=BC．
点评：掌握等腰梯形的判定和性质．
练习册系列答案
快乐5加2金卷系列答案
相关题目
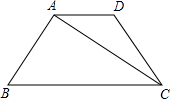已知：如图，在梯形ABCD中，AD∥BC，AB=DC，∠D=120°，对角线CA平分∠BCD，且梯形的周长为20，求AC的长及梯形面积S．
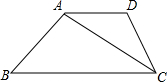已知：如图，在梯形ABCD中，AD∥BC，∠B=45°，∠BAC=105°，AD=CD=4，
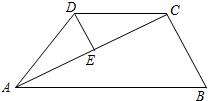已知：如图，在梯形ABCD中，AB∥CD，AC⊥BC，AC平分∠DAB，点E为AC的中点．求证：DE=
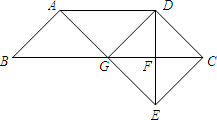（2013•闵行区二模）已知：如图，在梯形ABCD中，AD∥BC，AB=CD，BC=2AD．DE⊥BC，垂足为点F，且F是DE的中点，联结AE，交边BC于点G．
已知：如图，在梯形ABCD中，AD∥BC，CD=10cm，∠B=45度，∠C=30度，AD=5cm．