题目内容
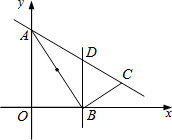 已知A(0,6),点B(t,0)是x轴正半轴上的一个动点,连接AB,作BC⊥AB,且BC:AB=1:2.又BD⊥x轴交直线AC于点D.
已知A(0,6),点B(t,0)是x轴正半轴上的一个动点,连接AB,作BC⊥AB,且BC:AB=1:2.又BD⊥x轴交直线AC于点D.
(1)如图,用含t的代数式表示点C的坐标及△ABC的面积;
(2)当△ABD为等腰三角形时,求出所有符合条件的点B的坐标.
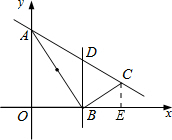 解:(1)过点C作CE⊥OB于E.
解:(1)过点C作CE⊥OB于E.在△AOB与△BEC中,
∵∠AOB=∠BEC=90°,∠ABO=∠BCE=90°-∠CBE,
∴△AOB∽△BEC,
∴
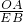 =
=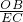 =
= =2,
=2,即
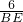 =
=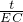 =2,
=2,∴BE=3,EC=
 t,
t,∴OE=OB+BE=t+3,
∴点C的坐标为(t+3,
 t);
t);在Rt△BCE中,BC2=CE2+BE2=
 t2+9,
t2+9,∵AB⊥BC,AB=2BC,
∴S△ABC=
 AB•BC=BC2,
AB•BC=BC2,∴S△ABC=
 t2+9;
t2+9;(2)∵A(0,6),C(t+3,
 t);
t);∴直线AC的解析式为y=
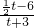 x+6.
x+6.∵点B(t,0),
∴设D(t,
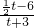 t+6),
t+6),∴AB2=t2+36,AD2=t2+(
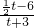 t)2,BD2=(
t)2,BD2=(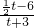 t+6)2.
t+6)2.分三种情况:
①当AD=AB时,t2+(
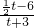 t)2=t2+36,(
t)2=t2+36,(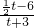 t)2=36,
t)2=36,∴
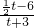 t=6或
t=6或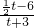 t=-6,
t=-6,当
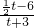 t=6时,整理得t2-24t-36=0,
t=6时,整理得t2-24t-36=0,解得t1=12+6
 ,t2=12-6
,t2=12-6 (不合题意,舍去),
(不合题意,舍去),∴B1(12+6
 ,0);
,0);当
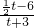 t=-6时,整理得t2+36=0,
t=-6时,整理得t2+36=0,此方程无解;
②当AD=BD时,t2+(
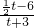 t)2=(
t)2=(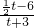 t+6)2,
t+6)2,整理得t3-3t2+36t-108=0,
∴(t-3)(t2+36)=0,
解得t=3,
∴B2(3,0);
③当AB=BD时,t2+36=(
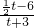 t+6)2,
t+6)2,整理得t3+8t2+36t+288=0,
∴(t+8)(t2+36)=0,
解得t=-8(不合题意,舍去).
综上可知,符合条件的点B的坐标为B1(12+6
 ,0),B2(3,0).
,0),B2(3,0).分析:(1)过点C作CE⊥OB于E,根据有两角对应相等的两三角形相似得出△AOB∽△BEC,列出比例式求出BE=3,EC=
 t,进而得到点C的坐标;先由勾股定理求出BC2,再根据三角形的面积公式及AB=2BC,得出S△ABC=BC2;
t,进而得到点C的坐标;先由勾股定理求出BC2,再根据三角形的面积公式及AB=2BC,得出S△ABC=BC2;(2)当△ABD为等腰三角形时,分三种情况:①AD=AB;②AD=BD;③AB=BD.每一种情况,都可以根据两点间距离公式列出关于t的方程,解方程即可.
点评:本题考查了一次函数的综合题,涉及到相似三角形的判定与性质,三角形的面积,勾股定理,等腰三角形的性质,一次函数解析式的确定,方程的解法等知识,注意(2)中,进行分类讨论是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目

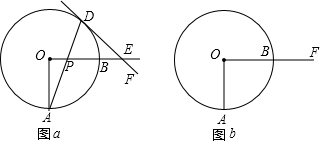
 18、已知三角形ABC.
18、已知三角形ABC. (1)画出△ABC关于点O的中心对称图形△DEF.
(1)画出△ABC关于点O的中心对称图形△DEF.