题目内容
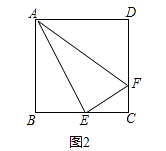
【题目】如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 . 
【答案】![]()
【解析】解:∵四边形ABCD是矩形, ∴AB=DC=1,∠B=∠C=90°,AD∥BC,AD=BC,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
∴∠DEA=∠DEM=90°,
在△ABM和△DEA中,  ,
,
∴△ABM≌△DEA(AAS),
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
连接DM,如图所示:
在Rt△DEM和Rt△DCM中, ![]() ,
,
∴Rt△DEM≌Rt△DCM(HL),
∴EM=CM,
∴BC=3CM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在Rt△ABM中,由勾股定理得:12+(2x)2=(3x)2 ,
解得:x= ![]() ,
,
∴BM= ![]() ;
;
故答案为: ![]() .
.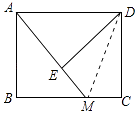
由AAS证明△ABM≌△DEA,得出AM=AD,证出BC=AD=3EM,连接DM,由HL证明Rt△DEM≌Rt△DCM,得出EM=CM,因此BC=3CM,设EM=CM=x,则BM=2x,AM=BC=3x,在Rt△ABM中,由勾股定理得出方程,解方程即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目