题目内容
(2012•长春一模)从水平地面到水平观景台之间有一段台阶路和一段坡路,示意图如下.台阶路AE共有8个台阶,每个台阶的宽度均为0.5m,台阶路AE与水平地面夹角∠EAB为28°.坡路EC长7m,与观景台地面的夹角∠ECD为15°.求观景台地面 CD距水平地面AB的高度BD (精确到0.1m).
CD距水平地面AB的高度BD (精确到0.1m).
[参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53;sin15°=0.26,cos15°=0.97,tan15°=0.27].
 CD距水平地面AB的高度BD (精确到0.1m).
CD距水平地面AB的高度BD (精确到0.1m).[参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53;sin15°=0.26,cos15°=0.97,tan15°=0.27].
分析:作EM⊥CD于M,EN⊥AB于N,在直角三角形ANE中求出EN的值,在直角三角形CME中,求出ME的值,进而求出BD的长.
解答:解:作EM⊥CD于M,EN⊥AB于N.
在△ANE中,∠ENA=90°,tan∠EAN=
,
∵∠BAE=28°,AN=0.5×8=4m,
∴EN=AN•tan28°=4×0.53=2.12m,
在△CME中,∠CME=90°,
sin∠ECM=
,
∵∠DCE=15°,EC=7m,
∴ME=CE•sin15°=7×0.26=1.82m,
∴NE+ME=2.12+1.82=3.94m,
答:观景台地面CD距水平地面AB的高度BD约3.9m.
在△ANE中,∠ENA=90°,tan∠EAN=
| EN |
| AN |

∵∠BAE=28°,AN=0.5×8=4m,
∴EN=AN•tan28°=4×0.53=2.12m,
在△CME中,∠CME=90°,
sin∠ECM=
| ME |
| CE |
∵∠DCE=15°,EC=7m,
∴ME=CE•sin15°=7×0.26=1.82m,
∴NE+ME=2.12+1.82=3.94m,
答:观景台地面CD距水平地面AB的高度BD约3.9m.
点评:此题考查了解直角三角形的知识,解答本题的关键是熟练掌握三角函数在解直角三角形的应用,求出涉及的线段长度,难度一般.

练习册系列答案
相关题目
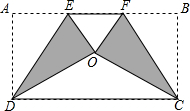 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x- -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)