Question

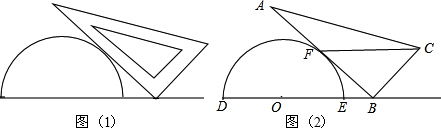
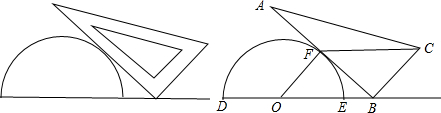
将一个量角器和一个含30度角的直角三角板如图（1）放置，图（2）是由他抽象出的几何图形，其中点B在半圆O的直径DE的延长线上，AB切半圆O于点F，且BC=OD。
（1）求证：DB∥CF。
（2）当OD=2时，若以O、B、F为顶点的三角形与△ABC相似，求弧的长度。

Answer 1

证明：（1）连接OF，如图     ∵AB切半圆O于F，    ∴OF⊥AB    ∵CB⊥AB ，    ∴BC∥OF。     ∵BC=OD，OD=OF，     ∴BC=OF。     ∴四边形OBCF是平行四边形，      ∴DB∥CF。 （2） ∵以O、B、F为顶点的三角形与△ABC相似，        ∠OFB=∠ABC=90°，     ∵∠OBF=∠BFC，∠BFC＞∠A，     ∴∠OBF＞∠A ∴∠OBF与∠A不可能是对应角     ∴∠A与∠BOF是对应角。     ∴∠BOF=30° 弧的长度=