题目内容
(1)在实数范围内分解因式:x2-3=______.
(2)已知 是整数,则正整数n的最小值是______.
是整数,则正整数n的最小值是______.
解:(1)x2-3=(x+ )(x-
)(x- );
);
(2)当n=3时, =
= =6,符合题意.
=6,符合题意.
故答案为:(1)(x+ )(x-
)(x- );(2)3
);(2)3
分析:(1)利用平方差公式分解即可得到结果;
(2)根据题意得到12n为完全平方数,n为最小的正整数,开方结果为整数,即可确定出n=3.
点评:此题考查了实数范围内分解因式,以及二次根式的定义,弄清题意是解本题的关键.
 )(x-
)(x- );
);(2)当n=3时,
 =
= =6,符合题意.
=6,符合题意.故答案为:(1)(x+
 )(x-
)(x- );(2)3
);(2)3分析:(1)利用平方差公式分解即可得到结果;
(2)根据题意得到12n为完全平方数,n为最小的正整数,开方结果为整数,即可确定出n=3.
点评:此题考查了实数范围内分解因式,以及二次根式的定义,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
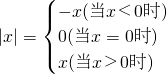 ,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和
,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和 分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②
分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②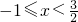 ③
③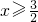 ,从而解方程|x+1|+|2x-3|=5可分以下三种情况:
,从而解方程|x+1|+|2x-3|=5可分以下三种情况: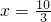 .
.