题目内容
 (2013•宜宾)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足
(2013•宜宾)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足| CF |
| FD |
| 1 |
| 3 |
①△ADF∽△AED;②FG=2;③tan∠E=
| ||
| 2 |
| 5 |
其中正确的是
①②④
①②④
(写出所有正确结论的序号).分析:①由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得:
=
,DG=CG,继而证得△ADF∽△AED;
②由
=
,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;
③由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=
;
④首先求得△ADF的面积,由相似三角形面积的比等于相似比,即可求得△ADE的面积,继而求得S△DEF=4
.
 |
| AD |
 |
| CD |
②由
| CF |
| FD |
| 1 |
| 3 |
③由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E=
| ||
| 4 |
④首先求得△ADF的面积,由相似三角形面积的比等于相似比,即可求得△ADE的面积,继而求得S△DEF=4
| 5 |
解答:解:①∵AB是⊙O的直径,弦CD⊥AB,
∴
=
,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵
=
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG-CF=2;
故②正确;
③∵AF=3,FG=2,
∴AG=
=
,
∴在Rt△AGD中,tan∠ADG=
=
,
∴tan∠E=
;
故③错误;
④∵DF=DG+FG=6,AD=
=
,
∴S△ADF=
DF•AG=
×6×
=3
,
∵△ADF∽△AED,
∴
=(
)2,
∴
=
,
∴S△AED=7
,
∴S△DEF=S△AED-S△ADF=4
;
故④正确.
故答案为:①②④.
∴
 |
| AD |
 |
| CD |
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵
| CF |
| FD |
| 1 |
| 3 |
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG-CF=2;
故②正确;
③∵AF=3,FG=2,
∴AG=
| AF2-FG2 |
| 5 |
∴在Rt△AGD中,tan∠ADG=
| AG |
| DG |
| ||
| 4 |
∴tan∠E=
| ||
| 4 |
故③错误;
④∵DF=DG+FG=6,AD=
| AG2+DG2 |
| 21 |
∴S△ADF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∵△ADF∽△AED,
∴
| S△ADF |
| S△AED |
| AF |
| AD |
∴
3
| ||
| S△AED |
| 3 |
| 7 |
∴S△AED=7
| 5 |
∴S△DEF=S△AED-S△ADF=4
| 5 |
故④正确.
故答案为:①②④.
点评:此题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
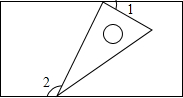 (2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=
(2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=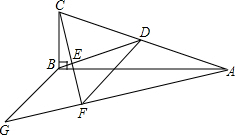 (2013•宜宾)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为
(2013•宜宾)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为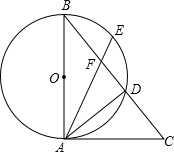 (2013•宜宾)如图,AB是⊙O的直径,∠B=∠CAD.
(2013•宜宾)如图,AB是⊙O的直径,∠B=∠CAD. (2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
(2013•宜宾)如图,抛物线y1=x2-1交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.