Question

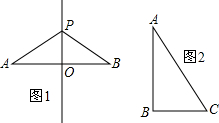
（1）如图①，已知C是线段AB上一点，分别以AC、BC为边长在AB的同侧作等边△ADC与等边△CBE，试猜想AE与DB的大小关系，并证明.

（2）如图②，当等边△CBE绕点C旋转后，上述结论是否仍成立？若成立，请证明；若不成立，请说明理由

Answer 1

（1）AE=BD（2）成立，证明见解析解析:
（1）证明：∵等边△ADC和△BCE，
∴AC=CD，BC=CE，∠DCA=∠ECB=60°，
∴∠DCA+∠DCE=∠ECB+∠DCE，
∴∠ACE=∠DCB，
在△ACE和△DCB中
AC="DC" ∠ACE=∠DCB CE=BC  ，
∴△ACE≌△DCB，
∴AE=BD．
（2）不论旋转多少度，AC=CD，BC=CE，∠DCA=∠ECB=60°，
推出∠ACE=∠BCD，
∴△ACE≌△DCB，
∴AE=BD．
（1）根据等边三角形性质推出AC=CD，BC=CE，∠DCA=∠ECB=60°，求出∠ACE=∠DCB，根据SAS证△ACE≌△DCB即可
（2）成立，根据（1）的推理过程即可得出答案