题目内容
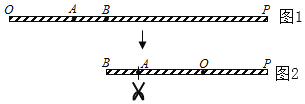
【题目】如图1，OP为一条拉直的细线，长为7cm，A，B两点在OP上，若先握住点B，将OB折向BP，使得OB重叠在BP上，如图
再从图2的A点及与A点重叠处一起剪开，使得细线分成三段
若这三段的长度由短到长之比为1：2：4，其中以点P为一端的那段细线最长，则OB的长为______cm．
【答案】2或
【解析】
根据题意可知剪断后的三段可以表示为OA、2AB、
，而根据题设可设三段分别为m，2m，4m，由总长度为7cm求出m的值，再分两种情况讨论
或
，从而求出各线段的长．
由题意可知剪断后的三段可以表示为OA、2AB、，
而这三段的长度由短到长之比为1：2：4，于是可设三段分别为m，2m，4m
即
剪断后的三条线段的长分别为1cm，2cm，4cm
又
以点P为一端的那段细线最长
，于是分类
若
，则
，
，
此时
若
，则
，
，
，
此时
故答案为2或．
练习册系列答案
相关题目
