题目内容
一个两位数，它的十位上数字为a，个位上数字为b，把a，b位置交换后，所得的两位数与原来的两位数之和是
11a+11b
11a+11b
．分析：由十位上的数字乘以10，加上个位上的数字表示出原来的两位数；以及交换后的两位数，将表示出的两个数字相加，去括号合并即可得到结果．
解答：解：根据题意得：原来的两位数为10a+b，交换后的两位数为10b+a，
则所得的两位数与原来的两位数之和是
（10a+b）+（10b+a）
=10a+b+10b+a
=11a+11b．
故答案为：11a+11b．
则所得的两位数与原来的两位数之和是
（10a+b）+（10b+a）
=10a+b+10b+a
=11a+11b．
故答案为：11a+11b．
点评：此题考查了整式的加减运算，以及列代数式，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．
练习册系列答案
相关题目
已知一个两位数，它的十位上的数字x比个位上的数字y大1，若对调个位与十位上的数字，得到的新数比原数小9，求这个两位数，所列方程组正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
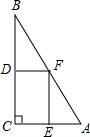（2013•仓山区模拟）（1）如图，在△ABC中，∠C=90°，BC＞AC，点D、E、F分别是△ABC三边的中点，求证：四边形DCEF是矩形．