题目内容
【题目】如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是_____________;
(2)三角形(2016)的直角顶点的坐标是_____________.
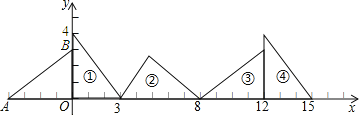
【答案】 6; (8064,0).
【解析】(1)根据点A、B的坐标求出OA、OB,再根据三角形的面积列式计算即可得解;
(2)观察不难发现,每3个三角形为一个循环组依次循环,用2013除以3,根据商是671可知三角形(2013)是第671个循环组的最后一个三角形,直角顶点在x轴上,再根据一个循环组的距离为12,进行计算即可得解.
解:(1)∵A(-4,0),B(0,3),
∴OA=4,OB=3,
∴△AOB的面积=![]() ×4×3=6;
×4×3=6;
(2)由图可知,每3个三角形为一个循环组依次循环,
∵2016=3×672,
∴三角形2016与三角形1的状态一样,
∴三角形2016的直角顶点的横坐标=672×12=8064,
∴三角形2016的顶点坐标为(8064, 0).
故答案为(8064,0).
“点睛”本题考查了坐标与图形变化-旋转,三角形的面积,仔细观察图形,发现每3个三角形为一个循环组依次循环是解题的关键,也是本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目