题目内容
16. 如图,在Rt△ABC中,∠BAC=90°
如图,在Rt△ABC中,∠BAC=90°(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
分析 (1)根据题意作出图形,如图所示;
(2)BC与⊙P相切,理由为:过P作PD⊥BC,交BC于点P,利用角平分线定理得到PD=PA,而PA为圆P的半径,即可得证.
解答  解:(1)如图所示,⊙P为所求的圆;
解:(1)如图所示,⊙P为所求的圆;
(2)BC与⊙P相切,理由为:
过P作PD⊥BC,垂足为D,
∵CP为∠ACB的平分线,且PA⊥AC,PD⊥CB,
∴PD=PA,
∵PA为⊙P的半径.
∴BC与⊙P相切.
点评 此题考查了直线与圆的位置关系,以及作图-复杂作图,证明切线的方法有两种:一种是连接证明垂直;一种是作垂线,证明垂线段等于半径.

练习册系列答案
相关题目
6.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是( )
| A. | v=320t | B. | v=$\frac{320}{t}$ | C. | v=20t | D. | v=$\frac{20}{t}$ |
4.某校进行书法比赛,有39名同学参加预赛,只能有19名同学参加决赛,他们预赛的成绩各不相同,其中一名同学想知道自己能否进入决赛,不仅要了解自己的预赛成绩,还要了解这39名同学预赛成绩的( )
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
1.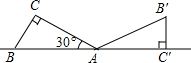 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |



