Question

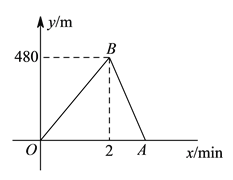
【题目】小明和小敏进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡脚跑到坡顶再原路返回坡脚．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的倍．设两人出发后距出发点的距离为ym．图中折线段表示小明在整个训练中y与x的函数关系．

（）点所表示的实际意义是__________．

（）求所在直线的函数表达式．

（）如果小敏上坡平均速度是小明上坡平均速度的一半，那么两人出发后多长时间第一次相遇？

Answer 1

【答案】（1）小明出发2分钟跑到坡顶，此时离坡脚480米；

（）AB所在直线的函数表达式为；

（）两人第一次相遇时间为．

【解析】试题分析：（1）根据到出发点的距离由大变小可知小亮2min时开始下坡返回；（2）求出下坡时的速度，然后求出下坡的时间，从而得到点A的坐标，设直线AB的解析式为y=kx+b，利用待定系数法求一次函数解析式解答；（3）设两人出发后xmin相遇，根据第一次相遇时，小敏下坡，小明上坡，列出方程求解即可．

试题解析：（）小明出发分钟跑到坡顶，此时离坡脚米．

（）小明上坡的平均速度为 ，

则其下坡的平均速度为 ，

故回到出发点时间为 ．

所以点坐标为，

设所在直线的函数表达式为，

因为的图像过点、，

所以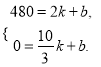

解方程组，得

所以所在直线的函数表达式为．

（）根据题意，可知小敏上坡的平均速度为，

设小敏出发后距出发点的距离为，

所以，解方程组得

因此，两人第一次相遇时间为．