Question

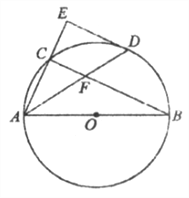
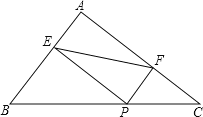
【题目】如图，在△ABC中，AD平分∠BAC交BC于点D，F为AD上一点，且BF＝BD．BF的延长线交AC于点E．

（1）求证：ABAD＝AFAC；

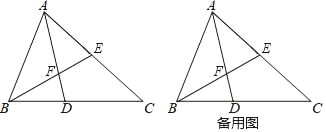
（2）若∠BAC＝60°．AB＝4，AC＝6，求DF的长；

（3）若∠BAC＝60°，∠ACB＝45°，直接写出的值．

Answer 1

【答案】（1）证明见解析；（2）；（3）

【解析】

（1）证△AFB∽△ADC即可

（2）作BH⊥AD于H，作CN⊥AD于N，则BH＝AB＝2，CN＝AC＝3，再证△BHD∽△CND即可

（3）易证△ABD，△AEF，△BFD均为顶角为30°的等腰三角形，即可根据△ABD∽△AEF和（1）中△AFB∽△ADC得，即可求．

解：

（1）∵AD平分∠BAC

∴∠BAF＝∠DAC

又∵BF＝BD

∴∠BFD＝∠FDB

∴∠AFB＝∠ADC

∴△AFB∽△ADC

∴．

∴ABAD＝AFAC

（2）作BH⊥AD于H，作CN⊥AD于N，则BH＝AB＝2，CN＝AC＝3

∴AH＝BH＝2，AN＝CN＝3

∴HN＝

∵∠BHD＝∠CDN

∴△BHD∽△CND

∴

∴HD＝

又∵BF＝BD，BH⊥DF

∴DF＝2HD＝

（3）由（1）得①，易证△ABD，△AEF，△BFD均为顶角为30°的等腰三角形

∴AH＝AD，AE＝AF，BF＝BD

易证△ABD∽△AEF

∴②

∴①×②得，过F作FG⊥AB于G，设FG＝x，则AF＝2x，BF＝x，AG＝x，BG＝x

∴AB＝（+1）x，

∴＝4﹣2