Question

点A（2，a）在正比例函数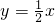的图象上，一次函数y=2x-3的图象与x轴交于点B，O为坐标原点，则△AOB的面积等于________．

Answer 1

分析：先将A点坐标代入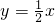，求出a的值，得到点A（2，1），再将y=0代入y=2x-3，求出x的值，得到点B（0，），那么△AOB可看作底边是线段OB的长，高是点A的横坐标2，利用三角形的面积公式即可求解．
解答：∵点A（2，a）在正比例函数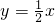的图象上，
∴a=×2=1，即A（2，1）．
∵y=2x-3，令y=0，得x=，即B（0，）．
∴S_△AOB=×OB×2=××2=．
故答案为．
点评：此题主要考查了一次函数图象上点的坐标特征以及三角形的面积，正确求出点A与点B的坐标是解题的关键．