题目内容
 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积是
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积是5
5
.分析:过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,得CF=1,DF=2.根据勾股定理可求CD2得正方形的面积.
解答: 解:作EF⊥l2,交l1于E点,交l4于F点.
解:作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠AED=∠DFC=90°.
∵ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
∴△ADE≌△DCF,
∴CF=DE=1.
∵DF=2,
∴CD2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
 解:作EF⊥l2,交l1于E点,交l4于F点.
解:作EF⊥l2,交l1于E点,交l4于F点.∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠AED=∠DFC=90°.
∵ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
∴△ADE≌△DCF,
∴CF=DE=1.
∵DF=2,
∴CD2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
点评:题考查正方形的性质和面积计算,根据平行线之间的距离构造全等的直角三角形是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( )
6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( ) (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )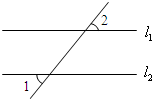 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= 如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.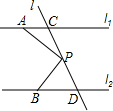 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.