题目内容
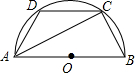
如图四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若再增加一个条件，就可使四边形ABCD成为等腰梯形，你所增加的条件是（只写出一个条件，图中不再增加其他的字母和线段．（给出证明）
添加的条件为
=
；
证明：∵四边形ABCD是圆的内接四边形，
∴∠A+∠C=180°；
∵
=
，
∴
=
；
∴∠A=∠B；
∴∠B+∠C=180°；
∴AB∥CD；
∵
=
，
∴AD=BC；
又∵AB＞CD，
∴四边形ABCD是等腰梯形．
 |
| AD |
|
| BC |
证明：∵四边形ABCD是圆的内接四边形，
∴∠A+∠C=180°；
∵
|
| AD |
|
| BC |
∴
|
| ADC |
|
| BCD |
∴∠A=∠B；
∴∠B+∠C=180°；
∴AB∥CD；
∵
|
| AD |
|
| BC |
∴AD=BC；
又∵AB＞CD，
∴四边形ABCD是等腰梯形．
练习册系列答案
相关题目
点E、F分别位于所在线段的什么位置？并证明你的结论（证明一种情况即可）．
