题目内容
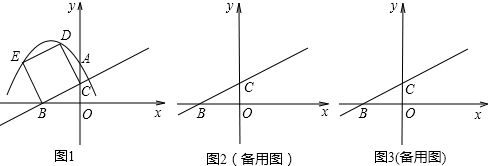
如图1,在直角坐标系中,已知点A(0,2)、点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.(1)填空:点D的坐标为______,点E的坐标为______.
(2)若抛物线y=ax2+bx+c(a≠0)经过A、D、E三点,求该抛物线的解析式.
(3)若正方形和抛物线均以每秒
 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.①在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围.
②运动停止时,求抛物线的顶点坐标.

【答案】分析:(1)构造全等三角形,由全等三角形对应线段之间的相等关系,求出点D、点E的坐标;
(2)利用待定系数法求出抛物线的解析式;
(3)本问非常复杂,须小心思考与计算:
①为求s的表达式,需要识别正方形(与抛物线)的运动过程.正方形的平移,从开始到结束,总共历时 秒,期间可以划分成三个阶段:当0<t≤
秒,期间可以划分成三个阶段:当0<t≤ 时,对应图(3)a;当
时,对应图(3)a;当 <t≤1时,对应图(3)b;当1<t≤
<t≤1时,对应图(3)b;当1<t≤ 时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;
时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;
②当运动停止时,点E到达y轴,点E(-3,2)运动到点E′(0, ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.
个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.
解答: 解:(1)由题意可知:OB=2,OC=1.
解:(1)由题意可知:OB=2,OC=1.
如图(1)所示,过D点作DH⊥y轴于H,过E点作EG⊥x轴于G.
易证△CDH≌△BCO,∴DH=OC=1,CH=OB=2,∴D(-1,3);
同理△EBG≌△BCO,∴BG=OC=1,EG=OB=2,∴E(-3,2).
∴D(-1,3)、E(-3,2).
(2)抛物线经过(0,2)、(-1,3)、(-3,2),
则 ?
?
解得 ,
,
∴ .
.
(3)①当点D运动到y轴上时,t= .
.
当0<t≤ 时,如图(3)a所示.
时,如图(3)a所示.
设D′C′交y轴于点F
∵tan∠BCO= =2,又∵∠BCO=∠FCC′
=2,又∵∠BCO=∠FCC′
∴tan∠FCC′=2,即 =2
=2
∵CC′= t,∴FC′=2
t,∴FC′=2 t.?
t.?
∴S△CC′F?= CC′•FC′=
CC′•FC′= t×
t× t=5t2
t=5t2
当点B运动到点C时,t=1.
当 <t≤1时,如图(3)b所示.
<t≤1时,如图(3)b所示.
设D′E′交y轴于点G,过G作GH⊥B′C′于H.
在Rt△BOC中,BC=
∴GH= ,∴CH=
,∴CH= GH=
GH=
∵CC′= t,∴HC′=
t,∴HC′= t-
t- ,∴GD′=
,∴GD′= t-
t-
∴S梯形CC′D′G?= (
( t-
t- +
+ t)
t)  =5t-
=5t-
当点E运动到y轴上时,t= .
.
当1<t≤ 时,如图(3)c所示
时,如图(3)c所示
设D′E′、E′B′分别交y轴于点M、N
∵CC′= t,B′C′=
t,B′C′= ,
,
∴CB′= t-
t- ,?∴B′N=2CB′=
,?∴B′N=2CB′= t-
t-
∵B′E′= ,∴E′N=B′E′-B′N=
,∴E′N=B′E′-B′N= -
- t
t
∴E′M= E′N=
E′N= (
( -
- t)
t)
∴S△MNE′?= (
( -
- t)•
t)• (
( -
- t)=5t2-15t+
t)=5t2-15t+
∴S五边形B′C′D′MN?=S正方形B′C′D′E′?-S△MNE′?= (5t2-15t+
(5t2-15t+ )=-5t2+15t-
)=-5t2+15t-
综上所述,S与x的函数关系式为:
当0<t≤ 时,S=5t2
时,S=5t2
当 <t≤1时,S=5t
<t≤1时,S=5t
当1<t≤ 时,S=-5t2+15t
时,S=-5t2+15t
②当点E运动到点E′时,运动停止.如图(3)d所示
∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′
∴△BOC∽△E′B′C
∴
∵OB=2,B′E′=BC=
∴
∴CE′=
∴OE′=OC+CE′=1+ =
=
∴E′(0, )
)
由点E(-3,2)运动到点E′(0, ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.
个单位.
∵ =
= ?
?
∴原抛物线顶点坐标为( ,
, )
)
∴运动停止时,抛物线的顶点坐标为( ,
, ).
).
点评:本题是非常典型的动线型综合题,全面考查了初中数学代数几何的多个重要知识点,包括:二次函数的图象与性质、待定系数法求解析式、抛物线与几何变换(平移)、相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质等.难点在于第(3)问,识别正方形和抛物线平移过程的不同阶段是关键所在.作为中考压轴题,本题涉及考点众多,计算复杂,因而难度很大,对考生综合能力要求很高,具有很好的区分度.
(2)利用待定系数法求出抛物线的解析式;
(3)本问非常复杂,须小心思考与计算:
①为求s的表达式,需要识别正方形(与抛物线)的运动过程.正方形的平移,从开始到结束,总共历时
 秒,期间可以划分成三个阶段:当0<t≤
秒,期间可以划分成三个阶段:当0<t≤ 时,对应图(3)a;当
时,对应图(3)a;当 <t≤1时,对应图(3)b;当1<t≤
<t≤1时,对应图(3)b;当1<t≤ 时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;
时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考;②当运动停止时,点E到达y轴,点E(-3,2)运动到点E′(0,
 ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.
个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标.解答:
 解:(1)由题意可知:OB=2,OC=1.
解:(1)由题意可知:OB=2,OC=1.如图(1)所示,过D点作DH⊥y轴于H,过E点作EG⊥x轴于G.
易证△CDH≌△BCO,∴DH=OC=1,CH=OB=2,∴D(-1,3);
同理△EBG≌△BCO,∴BG=OC=1,EG=OB=2,∴E(-3,2).
∴D(-1,3)、E(-3,2).
(2)抛物线经过(0,2)、(-1,3)、(-3,2),
则
 ?
?解得
 ,
,∴
 .
.(3)①当点D运动到y轴上时,t=
 .
.
当0<t≤
 时,如图(3)a所示.
时,如图(3)a所示.设D′C′交y轴于点F
∵tan∠BCO=
 =2,又∵∠BCO=∠FCC′
=2,又∵∠BCO=∠FCC′∴tan∠FCC′=2,即
 =2
=2∵CC′=
 t,∴FC′=2
t,∴FC′=2 t.?
t.?∴S△CC′F?=
 CC′•FC′=
CC′•FC′= t×
t× t=5t2
t=5t2当点B运动到点C时,t=1.

当
 <t≤1时,如图(3)b所示.
<t≤1时,如图(3)b所示.设D′E′交y轴于点G,过G作GH⊥B′C′于H.
在Rt△BOC中,BC=

∴GH=
 ,∴CH=
,∴CH= GH=
GH=
∵CC′=
 t,∴HC′=
t,∴HC′= t-
t- ,∴GD′=
,∴GD′= t-
t-
∴S梯形CC′D′G?=
 (
( t-
t- +
+ t)
t)  =5t-
=5t-
当点E运动到y轴上时,t=
 .
.
当1<t≤
 时,如图(3)c所示
时,如图(3)c所示设D′E′、E′B′分别交y轴于点M、N
∵CC′=
 t,B′C′=
t,B′C′= ,
,∴CB′=
 t-
t- ,?∴B′N=2CB′=
,?∴B′N=2CB′= t-
t-
∵B′E′=
 ,∴E′N=B′E′-B′N=
,∴E′N=B′E′-B′N= -
- t
t∴E′M=
 E′N=
E′N= (
( -
- t)
t)∴S△MNE′?=
 (
( -
- t)•
t)• (
( -
- t)=5t2-15t+
t)=5t2-15t+
∴S五边形B′C′D′MN?=S正方形B′C′D′E′?-S△MNE′?=
 (5t2-15t+
(5t2-15t+ )=-5t2+15t-
)=-5t2+15t-
综上所述,S与x的函数关系式为:
当0<t≤
 时,S=5t2
时,S=5t2当
 <t≤1时,S=5t
<t≤1时,S=5t
当1<t≤
 时,S=-5t2+15t
时,S=-5t2+15t
②当点E运动到点E′时,运动停止.如图(3)d所示

∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′
∴△BOC∽△E′B′C
∴

∵OB=2,B′E′=BC=

∴

∴CE′=

∴OE′=OC+CE′=1+
 =
=
∴E′(0,
 )
)由点E(-3,2)运动到点E′(0,
 ),可知整条抛物线向右平移了3个单位,向上平移了
),可知整条抛物线向右平移了3个单位,向上平移了 个单位.
个单位.∵
 =
= ?
?∴原抛物线顶点坐标为(
 ,
, )
)∴运动停止时,抛物线的顶点坐标为(
 ,
, ).
).点评:本题是非常典型的动线型综合题,全面考查了初中数学代数几何的多个重要知识点,包括:二次函数的图象与性质、待定系数法求解析式、抛物线与几何变换(平移)、相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质等.难点在于第(3)问,识别正方形和抛物线平移过程的不同阶段是关键所在.作为中考压轴题,本题涉及考点众多,计算复杂,因而难度很大,对考生综合能力要求很高,具有很好的区分度.

练习册系列答案
相关题目
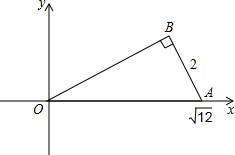 已知在Rt△OAB中,∠B=90°,
已知在Rt△OAB中,∠B=90°,
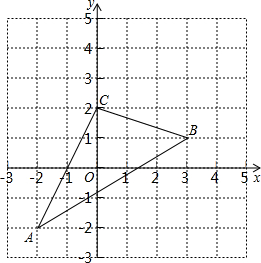 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,