Question

（本小题满分10分）如图，已知抛物线经过A（-2，0），B（-3，3）  及原点，顶点为．

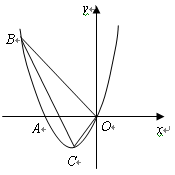
（1）求抛物线的解析式；

（2）若点在抛物线上，点在抛物线的对称轴上，且以A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；

（3）是抛物线上第一象限内的动点，过点作轴，垂足为，是否存在点，使得以、、为顶点的三角形与相似？若存在，求出点的坐标；若不存在，请说明理由．

 

Answer 1

解：（1）∵抛物线过原点，

∴可设抛物线的解析式为…………… 2分

（2）如图，①当为边时，

②当为对角线时，则与互相平分.

又点在对称轴上，

且线段的中点横坐标为-1，

由对称性知，符合条件的点只有一个，即顶点

综上所述，符合条件的点共有三个，分别为…… 6分

（3）存在. …………… 7分

如图，∵根据勾股定理得

∴

∴是直角三角形.

假设存在点，使得以为顶点的三角形与相似.

设，由题意知且

①若则

则  解得（舍去）.

当时，，即

综上所述，符合条件的点有两个，分别是…………… 10分

解析:略