题目内容
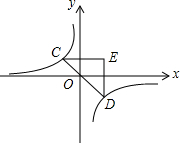 (2012•镇江二模)如图,已知点C为反比例函数y=-
(2012•镇江二模)如图,已知点C为反比例函数y=-| 6 | x |
12
12
.分析:CE交y轴于M点,DE交x轴于N点,连接OE,根据反比例函数y=
(k≠0)中比例系数k的几何意义得到S△OCM=S△ODN=
|k|=
×6=3,根据反比例函数图象的性质得到点C与点D关于原点中心对称,则OM=DN,CM=ON,于是CM=ME,所以S矩形OMEN=2S△OCM=6,然后计算△CDE的面积.
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:CE交y轴于M点,DE交x轴于N点,连接OE,如图,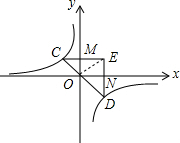
则S△OCM=S△ODN=
|k|=
×6=3,
∵C点与D点是正比例函数与反比例函数的交点,
∴点C与点D关于原点中心对称,
∴OM=DN,CM=ON,
∴CM=ME,
∴S矩形OMEN=2S△OCM=6,
∴S△CDE=3+6+3=12.
故答案为12.

则S△OCM=S△ODN=
| 1 |
| 2 |
| 1 |
| 2 |
∵C点与D点是正比例函数与反比例函数的交点,
∴点C与点D关于原点中心对称,
∴OM=DN,CM=ON,
∴CM=ME,
∴S矩形OMEN=2S△OCM=6,
∴S△CDE=3+6+3=12.
故答案为12.
点评:本题考查了反比例函数y=
(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
| k |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•镇江二模)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
(2012•镇江二模)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.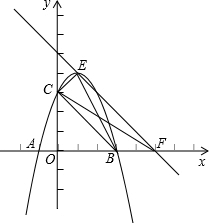 (2012•镇江二模)在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与y轴的正半轴交于点C,顶点为E.
(2012•镇江二模)在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与y轴的正半轴交于点C,顶点为E.