题目内容
如图，已知AB、AC分别是⊙O的直径和切线，BC交⊙O于D，AB=8，AC=6，则AD= ．
【答案】分析：由AB、AC分别是⊙O的直径和切线得∠CAB=∠ADB=90°，由勾股定理得BC=10，由三角形的面积公式求得AD=AC•AB÷BC=4.8．
解答：解：∵AB、AC分别是⊙O的直径和切线，
∴∠CAB=∠ADB=90°，
∵AB=8，AC=6，
∴BC=10，
∵AB•AC=BC•AD，
∴AD=AC•AB÷BC=4.8．
点评：本题利用了切线的性质，直径对的圆周角是直角，勾股定理，直角三角形的面积公式求解．
解答：解：∵AB、AC分别是⊙O的直径和切线，
∴∠CAB=∠ADB=90°，
∵AB=8，AC=6，
∴BC=10，
∵AB•AC=BC•AD，
∴AD=AC•AB÷BC=4.8．
点评：本题利用了切线的性质，直径对的圆周角是直角，勾股定理，直角三角形的面积公式求解．
练习册系列答案
相关题目
16、如图，已知AB、AC分别为⊙O的直径和弦，D为弧BC的中点，DE⊥AC于E．
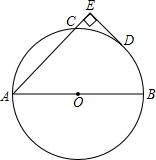如图，已知AB、AC分别为⊙O的直径和弦，D为弧BC的中点，DE⊥AC于E，DE=6，AC=16．
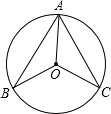如图，已知AB、AC是⊙O的两条弦，且AB=AC，若∠BOC=100°，则∠BAO=
（2008•宝山区二模）如图，已知AB、AC是⊙O的两条切线，切点分是点B、点C，∠BAC=60°，又⊙O的半径为2cm，则点A与点O的距离为
如图，已知AB：AC=AD：AE，∠BAD=∠CAE．求证：∠ABC=∠ADE．