题目内容
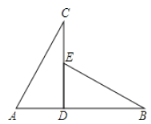
【题目】.如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB.设AP=x,△PBE的面积为y. 则能够正确反映
与
之间的函数关系的图象是
A. 
B. 
C. 
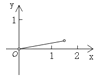D.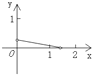 
【答案】A
【解析】
过点P作PF⊥BC于F，若要求△PBE的面积，则需要求出BE，PF的值，利用已知条件和正方形的性质以及勾股定理可求出BE，PF的值．再利用三角形的面积公式得到y与x的关系式，此时还要考虑到自变量x的取值范围和y的取值范围．
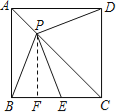
解：过点P作PF⊥BC于F，
∵PE=PB，
∴BF=EF，
∵正方形ABCD的边长是1，
∴AC=
=
，
∵AP=x，∴PC=-x，
∴PF=FC=
（-x）=1-x，
∴BF=FE=1-FC=x，
∴S△PBE=
BE?PF=x（1-x）=-x2+x，
即y=-x2+x（0＜x＜），
∴y是x的二次函数（0＜x＜），
故选A．
本题考查了动点问题的函数图象，和正方形的性质；等于直角三角形的性质；三角形的面积公式．对于此类问题来说是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．
【题目】小东根据学习函数的经验，对函数
的图象与性质进行了探究．下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数的自变量x的取值范围是 ；
（2）下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________；
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点. 根据描出的点，画出函数的大致图象；
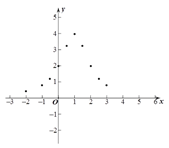
（4）结合函数图象，请写出函数的一条性质：______________________.
（5）解决问题：如果函数与直线y=a的交点有2个，那么a的取值范围是______________ .
