Question

2012年下半年起，某地区发生了特大旱情，为抗旱保丰收，某地政府制定民农户投资购买抗旱设备的补贴办法，其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额与政府补贴的额度存在下表所示的函数对应关系.

型 号 金 额	Ⅰ型设备		Ⅱ型设备
投资金额x（万元）	x	5	x	2	4
补贴金额y（万元）	y1=kx (k≠0)	2	y2=ax2+bx  (a≠0)	2.4	3.2

（1）分别求出和的函数解析式；

（2）有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买，请你设计一个能获得最大补贴金额的方案，并求出按此方案能获得的最大补贴金额.

Answer 1

1）由题意得：①5k=2，k=

∴                  2分

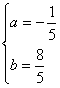②，解之得：，∴         6分

（2）设购Ⅱ型设备投资t万元，购Ⅰ型设备投资（10-t）万元，共获补贴Q万元

∴，

∴当t=3时，Q有最大值为，此时10-t=7(万元)

即投资7万元购Ⅰ型设备，投资3万元购Ⅱ型设备，共获最大补贴5.8万元.          10分