题目内容
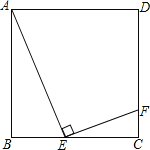
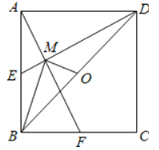
【题目】如图，已知
，
分别为正方形
的边
，
的中点，
与
交于点
，
为
的中点，则下列结论：①
，②
，③
，④
．其中正确结论的有（ ）
A.
个B.
个C.
个D.
个
【答案】B
【解析】
根据正方形的性质可得
，然后利用SAS即可证出
，根据全等三角形的性质可得：
，根据直角三角形的性质和三角形的内角和，即可判断①；根据中线的定义即可判断②；设正方形
的边长为
，根据相似三角形的判定证出
，列出比例式，即可判断③；过点
作
于
，易证△AMN∽△AFB，列出比例式，利用勾股定理求出ME、MF和MB即可判断④．
解：在正方形中，
，
，
、
分别为边
，
的中点，
，
在
和
中，
，
，
，
，
，
故①正确;
是
的中线，
，
，
故②错误;
设正方形的边长为，则
，
在
中，
，
，
，
，
，即
，
解得：
，
，
，
故③正确；
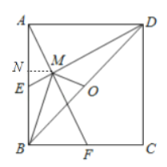
如图，过点作于，
∴
∴△AMN∽△AFB
∴
，
即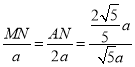
，
解得
，
，
根据勾股定理，
，
，
，故④正确.
综上所述，正确的结论有①③④共3个
故选：B．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
