题目内容
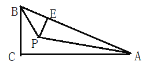
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，正方形DECF的三个顶点D，E，F分别落在边AB，AC，BC上．
（1）用尺规作出正方形DECF；
（2）求正方形DECF的边长．
【答案】（1）见解析；（2）
【解析】
（1）根据正方形的性质，先作∠ACB的平分线，得到点D，再分别过点D作AC和BC的垂线，得到点E和点F，顺次连接即可；
（2）设正方形的边长为x，根据题意证明△AED∽△ACB，得到
，求解即可.
解：（1）如图，
∴正方形DECF就是所求的；
（2）设正方形的边长为x，则AE=4－x，
在正方形DECF中，DE∥CF
∴∠AED=∠ACB，
∵∠A=∠A
∴△AED∽△ACB
∴
∴
∴x=
∴正方形DECF的边长为.
练习册系列答案
相关题目
