题目内容
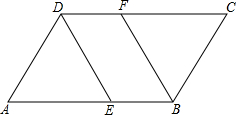 如图,∠ABC=∠ADC,DE,BF分别平分∠ADC,∠ABC,∠DEA=∠FBA,那么DF与BE平行吗?为什么?
如图,∠ABC=∠ADC,DE,BF分别平分∠ADC,∠ABC,∠DEA=∠FBA,那么DF与BE平行吗?为什么?
平行;
证明:∵DE,BF分别平分∠ADC,∠ABC,
∴∠FBA= ∠ABC,∠FDE=
∠ABC,∠FDE= ∠ADC,
∠ADC,
∵∠ABC=∠ADC,
∴∠FBA=∠CDE,
∵∠DEA=∠FBA,
∴∠DEA=∠CDE,
∴CD∥AB.
分析:首先证明∠FBA=∠CDE,再有条件∠DEA=∠FBA可得∠DEA=∠CDE,进而得到CD∥AB.
点评:此题主要考查了平行线的判定和性质,关键是掌握内错角相等两直线平行.
证明:∵DE,BF分别平分∠ADC,∠ABC,
∴∠FBA=
 ∠ABC,∠FDE=
∠ABC,∠FDE= ∠ADC,
∠ADC,∵∠ABC=∠ADC,
∴∠FBA=∠CDE,
∵∠DEA=∠FBA,
∴∠DEA=∠CDE,
∴CD∥AB.
分析:首先证明∠FBA=∠CDE,再有条件∠DEA=∠FBA可得∠DEA=∠CDE,进而得到CD∥AB.
点评:此题主要考查了平行线的判定和性质,关键是掌握内错角相等两直线平行.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
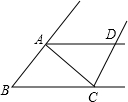 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
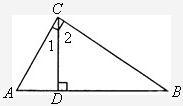
 ,且CB=CE.
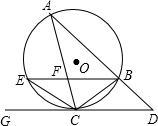
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.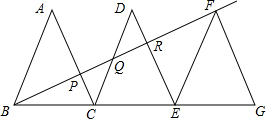 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且