题目内容
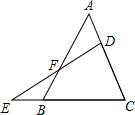如图，点D在AC上，点E在CB的延长线上，且BE=AD，ED交AB于点F，求证：EF•BC=AC•FD．
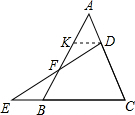证明：过点D作DK∥BC，交AB于点K，∴△AKD∽△ABC，△DKF∽△EBF，
∴
，
，∴
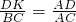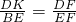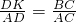，∵BE=AD，
∴
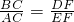，∴EF•BC=AC•FD．
分析：首先过点D作DK∥BC，交AB于点K，即可得△AKD∽△ABC，△DKF∽△EBF，然后由相似三角形的对应边成比例与比例变形，易证得
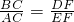，则可证得EF•BC=AC•FD．点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
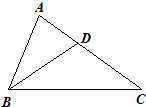21、如图，点D在AC上，且∠ABD=∠C，AB=4，CD=6，求AD的长．
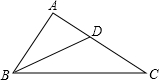如图，点D在AC上，且∠ABD=∠C，AB=CD=2，则AD=
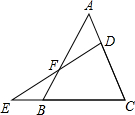如图，点D在AC上，点E在CB的延长线上，且BE=AD，ED交AB于点F，求证：EF•BC=AC•FD．
已知：如图，点O在AC上，⊙O过B，C两点，交AC于点D，AB与⊙O相切．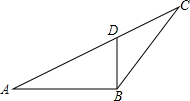
如图，点D在AC上，∠BAD=∠DBC．