题目内容
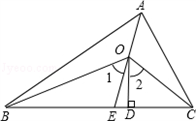
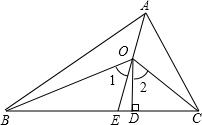 如图,AE、OB、OC分别平分∠BAC、∠ABC、∠ACB,OD⊥BC,求证:∠1=∠2.
如图,AE、OB、OC分别平分∠BAC、∠ABC、∠ACB,OD⊥BC,求证:∠1=∠2.
分析:根据角平分线的定义和三角形的一个外角等于和它不相邻的两个内角的和,∠1等于∠ABC与∠BAC的一半的和,∠2等于90°减去∠ACB的一半,而∠ABC、∠ACB、∠BAC三个角的一半等于90°,所以∠2等于∠ABC与∠BAC的一半的和,所以∠1与∠2相等.
解答:证明:∵AE、OB、OC分别平分∠BAC、∠ABC、∠ACB,
∴∠1=
∠ABC+
∠BAC=
(180°-∠ACB)=90°-
∠ACB,
∠2=90°-
∠ACB,
∴∠1=∠2.
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠2=90°-
| 1 |
| 2 |
∴∠1=∠2.
点评:本题主要考查三角形的外角性质和角平分线的定义,熟练掌握性质和概念并灵活运用是解题的关键.

练习册系列答案
相关题目
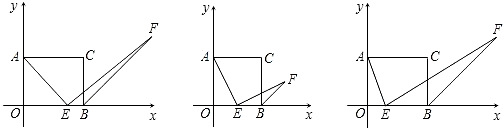
 ,MN=2
,MN=2
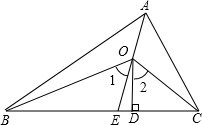 如图,AE、OB、OC分别平分∠BAC、∠ABC、∠ACB,OD⊥BC,求证:∠1=∠2.
如图,AE、OB、OC分别平分∠BAC、∠ABC、∠ACB,OD⊥BC,求证:∠1=∠2.