Question

（1）已知A=

1

x-2

，B=

2x

x2-4

，C=

2

x+2

．解方程A-B=C．
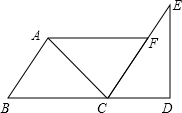
（2）如图，?ABCF中，∠BAC=90°，延长CF到E，使CE=BC，过E作BC的垂线，交延长线于点D．求证：AB=CD．

Answer 1

分析：（1）首先根据题意得到方程：

1

x-2

-

2x

x2-4

=

2

x+2

，解此分式方程即可求得答案，注意分式方程需要检验；
（2）由平行四边形的性质易得：∠B=∠DCE，又由ED⊥BC，∠BAC=90°，即可证得：△ABC≌△DCE，又由全等三角形的对应边相等，即可证得：AB=CD．

解答：解：（1）∵A-B=C，
∴

1

x-2

-

2x

x2-4

=

2

x+2

，
方程两边同乘以（x+2）（x-2），得：x+2-2x=2x-4，
解得：x=2，
检验：当x=2时，分母（x+2）（x-2）=0，∴x=2不是原方程的解．
∴原方程无解；

（2）证明：∵四边形ABCF是平行四边形，
∴AB∥CE，
∴∠B=∠DCE．
∵ED⊥BC，∠BAC=90°，
∴∠EDC=90°=∠BAC，
在△ABC和△DCE中，
CE=BC，∠B=∠DCE，∠EDC=∠BAC，
∴△ABC≌△DCE，
∴AB=CD．

点评：（1）考查了分式方程的求解方法，注意转化思想的应用，还要注意分式方程需要检验；
（2）考查了全等三角形的判定与性质以及平行四边形的性质，注意数形结合思想的应用．