Question

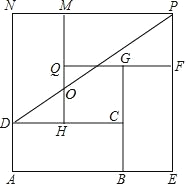
【题目】如图，已知长方形 ABCD 中，AB＝a，BC＝b．正方形 AEPN 是由长方形 ABCD经过图形的运动形成的．其中长方形 GBEF 是由长方形 ABCD 绕着 B 点顺时针旋转 90° 得到的，长方形 HMND 是由将长方形 ABCD 绕着 D 点逆时针旋转 90°得到的，长方形QFPM 是长方形 ABCD 经过平移得到的．

（1） 长方形 QFPM 是由长方形 ABCD 经过怎样平移得到的？

（2） 用含 a、b 的代数式分别表示正方形 HCGQ 的面积；

（3） 连接 DP，交 HM 于点 O．用 a、b 的代数式分别表示 OM．

Answer 1

【答案】（1）见解析；（2）S 正方形 HCGQ＝（a﹣b）2；（3 ）

【解析】

（1）根据平移的定义即可得到结论；

（2）根据正方形的面积公式即可得到结论；

（3）根据相似三角形的性质即可得到结论．

解：（1）长方形 QFPM 是由长方形 ABCD先向上平移a个单位，再向右平移b个单位得到；

（2）S 正方形 HCGQ＝（a﹣b）2；

（3 ）∵PN∥CD，∴△PMO∽△DHO，∴ ，

即 ∴OM＝