Question

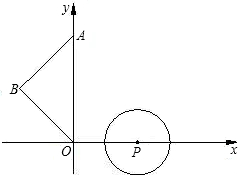
如图，平面直角坐标系中的△ABO与⊙P，若P、A、B三点的坐标分别为P（2，0）、A（0，2

3

）、B（-

3

，

3

），且⊙P的半径为1，完成下列问题：
（1）将△ABO绕点O顺时针旋转α角（α为锐角），使OA与⊙P相切，请在图中画出旋转后的△A′B′O，并求出旋转角α的大小；
（2）在（1）的情况下求A′、B′的坐标．

Answer 1

分析：（1）相切后可得∠PDO=90°，PD=1，OP=2，那么可得∠DOP的正弦值，进而判断出∠DOP的度数，就得到∠AOA'的度数，即为旋转角的度数；
（2）易得OA'=OA=2

3

，利用∠A'OE的三角函数值即可求得A'的横纵坐标；利用三角函数求得直角三角形B'HP各边的值，进而求得点B'的坐标．

解答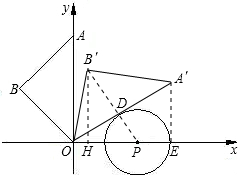：解：（1）连接DP，
∴∠PDO=90°，PD=1，OP=2，
∴sinDOP=PD：OP=0.5，
∴∠DOP=30°，
∴旋转角α=90°-∠DOP=60°；

（2）做A'E⊥x轴于点E，
∵OA'=OA=2

3

，∠DOP=30°，
∴A'E=

3

，OE=3，
∴A′（3，

3

）；
连接B'D，易得B'DP在一条直线上，做BH⊥x轴于点H，那么
B'P=

3

+1；
∵∠DPO=90°-∠DOP=60°，
∴HP=

3 +1

2

，B'H=

3 +3

2

，
∴OH=2-HP=

3- 3

2

，
∴B′（

3- 3

2

，

3+ 3

2

）．

点评：连接圆心和切点构造直角三角形是常见的辅助线方法，注意利用特殊三角函数求解．