Question

【题目】探究证明：

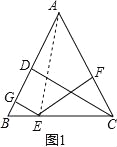
（1）如图1，在△ABC中，AB=AC，点E是BC上的一个动点，EG⊥AB，EF⊥AC，CD⊥AB，点G，F，D分别是垂足．求证：CD=EG+EF；

猜想探究：

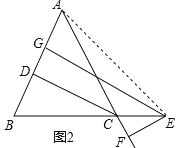
（2）如图2，在△ABC中，AB=AC，点E是BC的延长线上的一个动点，EG⊥AB于G，EF⊥AC交AC延长线于F，CD⊥AB于D，直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ；

问题解决：

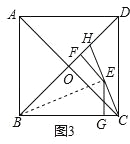
（3）如图3，边长为10的正方形ABCD的对角线相交于点O、H在BD上，且BH=BC，连接CH，点E是CH上一点，EF⊥BD于点F，EG⊥BC于点G，则EF+EG= ．

Answer 1

【答案】（1）证明见解析

（2）CD=EG﹣EF，

（3）5．

【解析】

试题分析：（1）根据S△ABC=S△ABE+S△ACE，得到ABCD=ABEG+ACEF，根据等式的性质即可得到结论；

（2）由于S△ABC=S△ABE﹣S△ACE，于是得到ABCD=ABEG﹣ACEF，根据等式的性质即可得到结论；

（3）根据正方形的性质得到AB=BC=10，∠ABC=90°，AC⊥BD，根据勾股定理得到AC=10，由于S△BCH=S△BCE+S△BHE，得到BHOC=BCEG+BHEF，根据等式的性质即可得到结论．

试题解析：（1）如图1，连接AE，

∵EG⊥AB，EF⊥AC，CD⊥AB，

∵S△ABC=S△ABE+S△ACE，

∴ABCD=ABEG+ACEF，

∵AB=AC，

∴CD=EG+EF；

（2）CD=EG﹣EF，

理由：连接AE，

∵EG⊥AB，EF⊥AC，CD⊥AB，

∵S△ABC=S△ABE﹣S△ACE，

∴ABCD=ABEG﹣ACEF，

∵AB=AC，

∴CD=EG﹣EF；

故答案为：CD=EG﹣EF；

（3）∵四边形ABCD是正方形，

∴AB=BC=10，∠ABC=90°，AC⊥BD，

∴AC=10，

∴OC=AC=5，

连接BE．

∵EF⊥BD于点F，EG⊥BC于点G，

∵S△BCH=S△BCE+S△BHE，

∴BHOC=BCEG+BHEF，

∴OC=EG+EF=5，

故答案为：5．