题目内容
在平面直角坐标系中描出下列各点A（2，1），B（0，1），C（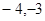
），D（6，
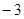），并将各点用线段一次连接构成一个四边形ABCD。
（1）四边形ABCD时什么特殊的四边形？
答：
（2）在四边形ABCD内找一点P，使得△APB、△BPC、△CPD、△APD都是等腰三角形，请写出P点的坐标。
【答案】
（1）如图，很容易判断四边形ABCD是等腰梯形，
那么点P一定在两底的垂直平分线上．
如果点P也在两腰的中垂线上，两腰的特殊性就在于它与坐标轴的夹角为45°，并且两腰的中点恰在格点上，从图形中很容易看出点P的坐标为（1，﹣4）．
设点P（1，y），显然只有DA=DP的可能了，
由两点间的距离公式，得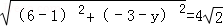
，
解得y=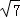
﹣3．
点P（1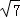，﹣3）在四边形ABCD内．
所以（1）等腰梯形；…………4分
（2）P（1，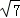
﹣3）．…………6分
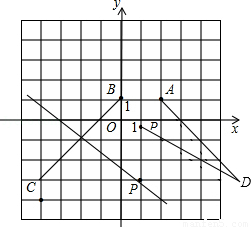
【解析】如图，很容易判断四边形ABCD是等腰梯形，那么点P一定在两底的垂直平分线上．如果点P也在两腰的中垂线上，两腰的特殊性就在于它与坐标轴的夹角为45°，并且两腰的中点恰在格点上，从图形中很容易看出点P的坐标为（﹣1，﹣4），设点P（1，y），显然只有DA=DP的可能了，由两点间的距离公式，得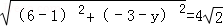，解得y=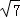﹣3．点P（1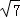，﹣3）在四边形ABCD内．
练习册系列答案
相关题目
当路况良好时，在干燥的路面上，汽车的刹车距离s与车速v之间的关系如下表所示：
（1）在平面直角坐标系中描出每对（v，s）所对应的点，并用光滑的曲线顺次连接各点；
（2）利用图象验证刹车距离s（m）与车速v（km/h）是否有如下关系：s=
v2+
v0；
（3）求当s=9m时的车速v．
| v/（km/h） | 40 | 60 | 80 | 100 | 120 |
| s/m | 2 | 4.2 | 7.2 | 11 | 15.6 |
（2）利用图象验证刹车距离s（m）与车速v（km/h）是否有如下关系：s=
| 1 |
| 1000 |
| 1 |
| 100 |
（3）求当s=9m时的车速v．
如图，在平面直角坐标系中描出4个点A（0，2），B（-1，0），C（1，-1），D（3，1）
某中学气象兴趣小组为了解某个山区气温随海拔高度的变化情况，现在在不同的海拔高度对气温进行了测量，记录数据如下：
①把上表中y=-
x+23的各组对应值作为点的坐标，在平面直角坐标系中描出相应的点，连接各点并观察所得的图形，猜测与x之间的函数关系，并求出函数关系式；
②已知某种杜鹃花适宜生长在平均气温为17～20℃的山区，估计适宜种植这种杜鹃花的山坡高度的范围．
| 海拔高度x（m） | 500 | 1500 | 2000 | 2500 |
| 气温y（℃） | 20 | 14 | 11 | 8 |
| 3 |
| 50 |
②已知某种杜鹃花适宜生长在平均气温为17～20℃的山区，估计适宜种植这种杜鹃花的山坡高度的范围．
构成一个四边形ABCD．
已知：A（-1，-2），B（3，2），C（0，4）