题目内容
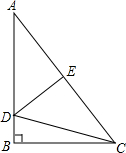
7.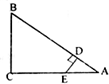 如图,Rt△ABC中,∠C=90°,AB=5,AC=4,E是AC上一点,AE=3,ED⊥AB,垂足为D.求DE的长和Sin∠DEA.
如图,Rt△ABC中,∠C=90°,AB=5,AC=4,E是AC上一点,AE=3,ED⊥AB,垂足为D.求DE的长和Sin∠DEA.
分析 根据勾股定理求出BC,根据相似三角形的判定得出△AED∽△ABC,根据相似三角形的性质得出$\frac{DE}{BC}$=$\frac{AE}{AB}$,∠DEA=∠B,即可得出答案.
解答 解:∵Rt△ABC中,AB=5,AC=4,
∴根据勾股定理:BC2=AB2-AC2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3,
∵ED⊥AB,
∴∠EDA=90°,
又∵∠C=90°,
∴∠EDA=∠C,
∵∠A=∠A,
∴△AED∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$,
∴DE=$\frac{BC•AE}{AB}$=$\frac{3×3}{5}$=$\frac{9}{5}$,
∵△AED∽△ABC,
∴∠DEA=∠B,
∴sin∠DEA=sin∠B=$\frac{AC}{AB}$=$\frac{4}{5}$.
点评 本题考查了勾股定理,相似三角形的性质和判定,解直角三角形的应用,能求出△AED∽△ABC是解此题的关键.

练习册系列答案
相关题目
17.下列图形中,轴对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.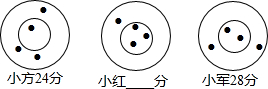 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )| A. | 30分 | B. | 32分 | C. | 33分 | D. | 34分 |
2.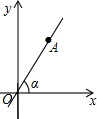 如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
 如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
17.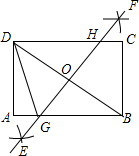 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )| A. | $\frac{25}{8}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{8}$ |
 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.