题目内容
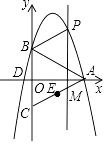
【题目】如图，已知CO1是△ABC的中线，过点O1作O1E1∥AC交BC于点E1 ， 连接AE1交CO1于点O2；过点O2作O2E2∥AC交BC于点E2 ， 连接AE2交CO1于点O3；过点O3作O3E3∥AC交BC于点E3 ， …，如此继续，可以依次得到点O4 ， O5 ， …，On和点E4 ， E5 ， …，En ． 则OnEn=AC．（用含n的代数式表示）
【答案】
【解析】解∵O1E1∥AC，
∴△BO1E1∽△BAC，
∴ 
，
∵O1是AB的中点，
∴BO1= 
AB，
∴ 
，
∴O1E1= 
，
∵O1E1∥AC，
∴△O1E1O2∽△CAO2，
∴ 
= ，
∴ 
= 
，
∵O2E2∥AC，
∴△E1O2E2∽△E1AC，
∴ 
= ，
∴O2E2= AC，
同理得： 
= 
，
O3E3= AC，
…
∴OnEn= AC，
故答案为： ．
本题考查了相似三角形的判定与性质以及三角形中位线定理，由O1E1∥AC可得出△BO1E1∽△BAC和△E1O1O2∽△ACO2，再由相似三角形的性质结合三角形中位线定理即可得到所求结论.
练习册系列答案
相关题目
