题目内容
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90° 证明:∵AB∥CD()
∴∠ABD+∠BDC=180°()
∵BE平分∠ABD()
∴∠EBD= ![]() ()
()
又∵DE平分∠BDC
∴∠BDE= ![]() ()
()
∴∠EBD+∠EDB= ![]() ∠ABD+
∠ABD+ ![]() ∠BDC()
∠BDC()
= ![]() (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.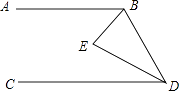
【答案】已知;两直线平行,同旁内角互补;已知;∠ABD;角平分线的定义;∠CDB;角平分线的定义;等式的性质
【解析】证明:∵AB∥CD(已知) ∴∠ABD+∠BDC=180°(两直线平行,同旁内角互补)
∵BE平分∠ABD(已知)
∴∠EBD= ![]() ∠ABD(角平分线的定义)
∠ABD(角平分线的定义)
又∵DE平分∠BDC
∴∠BDE= ![]() ∠CDB(角平分线的定义)
∠CDB(角平分线的定义)
∴∠EBD+∠EDB= ![]() ∠ABD+
∠ABD+ ![]() ∠BDC(等式的性质)
∠BDC(等式的性质)
= ![]() (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.
所以答案是:已知,两直线平行,同旁内角互补,已知,∠ABD,角平分线的定义,∠CDB,角平分线的定义,等式的性质
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目